Pravděpodobnost, míry a martingaly: úvod
📊 Souhrn
Přednáška představuje úvod do kurzu pokročilé teorie pravděpodobnosti, zaměřeného na míry a martingaly. Začíná přehledem známých konceptů, jako je jednoduchá symetrická náhodná procházka, a diskutuje různé typy konvergence náhodných veličin - konvergence v pravděpodobnosti, skoro jistá konvergence a konvergence v distribuci. Přednášející ilustruje tyto koncepty prostřednictvím vizualizací a uvádí důležité výsledky jako silný zákon velkých čísel, centrální limitní větu a zákon iterovaného logaritmu.
Druhá část přednášky se věnuje větvícím procesům (Galton-Watsonův proces), martingalům a jejich využití v matematické finance. Přednášející vysvětluje, jak lze pomocí martingalů určit spravedlivou cenu finančních instrumentů, a zavádí koncept změny míry. Přednáška končí naznačením, že v následujících týdnech kurz vybuduje jazyk teorie míry, aby bylo možné všechny zmíněné koncepty formálně definovat a dokázat. Cílem kurzu je nejen naučit se tyto koncepty, ale také dokázat jejich existenci a vlastnosti.
📝 Přepis
Úvod do kurzu a náhodná procházka
Dnes začínáme a budeme se věnovat rychlému přehledu různých věcí, které jste už možná viděli nebo které jsou těsně za hranicí vašeho dosavadního poznání. Cílem je rozvinout některé koncepty, které pak budeme potřebovat v průběhu celého kurzu.
Nejprve si povíme o jednoduché symetrické náhodné procházce. To už jste všichni viděli. S₀ se rovná 0, a pak Sₙ se rovná sumě od k=1 do n Xₖ. X_k jsou nezávislé stejně rozdělené náhodné veličiny představující kroky nahoru a dolů. Pravděpodobnost, že Xₖ je rovno +1, je jedna polovina. Pravděpodobnost, že Xₖ je rovno -1, je také jedna polovina.
Je zřejmé, co se děje - moje procházka dělá krok nahoru, nahoru, dolů, dolů, nahoru, dolů, dolů, dolů, nahoru. A tak to pokračuje. Je to suma nezávislých stejně rozdělených náhodných veličin a o těchto sumách jsme se už hodně naučili.
Konvergence náhodných veličin
První věc, kterou víte, je, že když se podíváte na empirický průměr, tedy na sumu prvních N proměnných dělenou N, tak tato hodnota konverguje. Konverguje k průměru každé z těchto náhodných veličin, což je v tomto případě nula.
Tento kód, který je dostupný online, simuluje jednoduchou symetrickou náhodnou procházku. Dělám 1 milion kroků a 30 tras. První graf nám ukazuje, že skutečně konvergujeme k nule.
V jakém smyslu konvergujeme k nule? Jednoduchý výrok, který byste měli znát z úvodu do pravděpodobnosti, by zněl, že konverguje v pravděpodobnosti. To znamená, že pravděpodobnost, že Sₙ děleno n je větší než epsilon, jde k nule, když n jde do nekonečna. To platí pro libovolné epsilon větší než nula.
Co je také pravdivé, je, že tato konvergence nastává skoro jistě. A to je mnohem silnější tvrzení. Statistika se na tom zakládá. Ale toto je z roku 1713, možná Bernoulliho první důkaz, a toto je z 30. let 20. století - Kolmogorov a Chinčin, takže mezi nimi uplynulo dobrých 300 let.
Jednou z věcí, které v tomto kurzu uděláme, je, že dokážeme toto tvrzení. Dokážeme, že suma nezávislých stejně rozdělených náhodných veličin dělená jejich počtem konverguje k jejich skutečnému průměru skoro jistě. Bude nám to trvat celý kurz. Tento důkaz možná přijde až v předposlední přednášce.
Centrální limitní věta a zákon iterovaného logaritmu
Jako matematik si položíte další otázku: Pokud vím, že to konverguje k nule, chtěl bych vědět, jak rychle to konverguje k nule. Co to znamená? Znamená to, že se budu dívat na Sₙ děleno n a vynásobím to něčím, co jde do nekonečna, abych dostal netriviální limit. Tímto “něčím” je odmocnina z n. A pak vím, že to konverguje k normální náhodné veličině v distribuci.
Nyní budu vykreslovat Sₙ děleno odmocninu z n. Každý člen je násoben odmocninou z n. Co to znamená? Znamená to, že pravděpodobnost, že tato Sₙ dělená odmocninou z n je větší než Φ⁻¹ (něčeho)… Co je Φ⁻¹? Podívám se na normální náhodnou veličinu a vezmu číslo. Toto je Φ⁻¹(0,95), takže dostanu celkem 10 % (při použití absolutní hodnoty).
Vykreslil jsem zde dvě čáry. Červená přerušovaná čára odpovídá Gaussově CDF na 0,98. Měl bych tedy dostat asi 4 % tras, které překročí červené čáry. To je u 30 tras asi 1,2 trasy, tedy něco málo přes jednu trasu. Vidíte tu černou trasu, která se téměř dotýká červené? Zelené čáry jsou to, co jsem napsal dříve, tedy by to mělo být asi 10 %, tedy asi čtyři trasy překračující zelené čáry. A v této simulaci jsem skutečně dostal černou, oranžovou a dvě trasy na spodním okraji.
Zákon iterovaného logaritmu
I když je to vzácné, budou existovat trasy, které půjdou hodně daleko, protože jde o normální náhodnou veličinu. Chtěl bych lépe pochopit, co to znamená. Výsledek, který jsme viděli dříve, je znám jako silný zákon velkých čísel. Tento výsledek je známý jako centrální limitní věta.
Nyní potřebuji něco trochu přesnějšího. Chtěl bych tvrzení, které mi řekne, jak přesně kontrolovat ty velmi vzácné trasy, které přesto porostou do nekonečna. Správné měřítko bude log log n. Ukáže se, že pokud to uděláme, tak tato veličina už nebude mít limit. Bude mít horní limit (lim sup), který se bude rovnat odmocnině ze 2, a bude mít dolní limit (lim inf), který se bude rovnat minus odmocnině ze 2.
Nyní místo dělení odmocninou z n dělím odmocninou z n krát log log n. A vykresluji minus a plus odmocninu ze 2. Ale stále jdu jen na milion kroků. Toto je skutečně asymptotický výsledek. K jeho pozorování byste měli běžet simulaci mnohem déle. Kód máte k dispozici a je velmi snadné ho upravit.
Toto je skutečně jemný výsledek - zákon iterovaného logaritmu. Log log n. To vám skutečně říká něco velmi specifického o chování vaší náhodné procházky. Možná to dokážeme, záleží na tom, jak strukturuji poslední dvě nebo tři přednášky. Ale budete mít nástroje k jeho dokázání.
Větvící procesy
Pojďme nyní mluvit o jiném procesu. Toto byl jednoduchá symetrická náhodná procházka. Nyní to bude větvící proces.
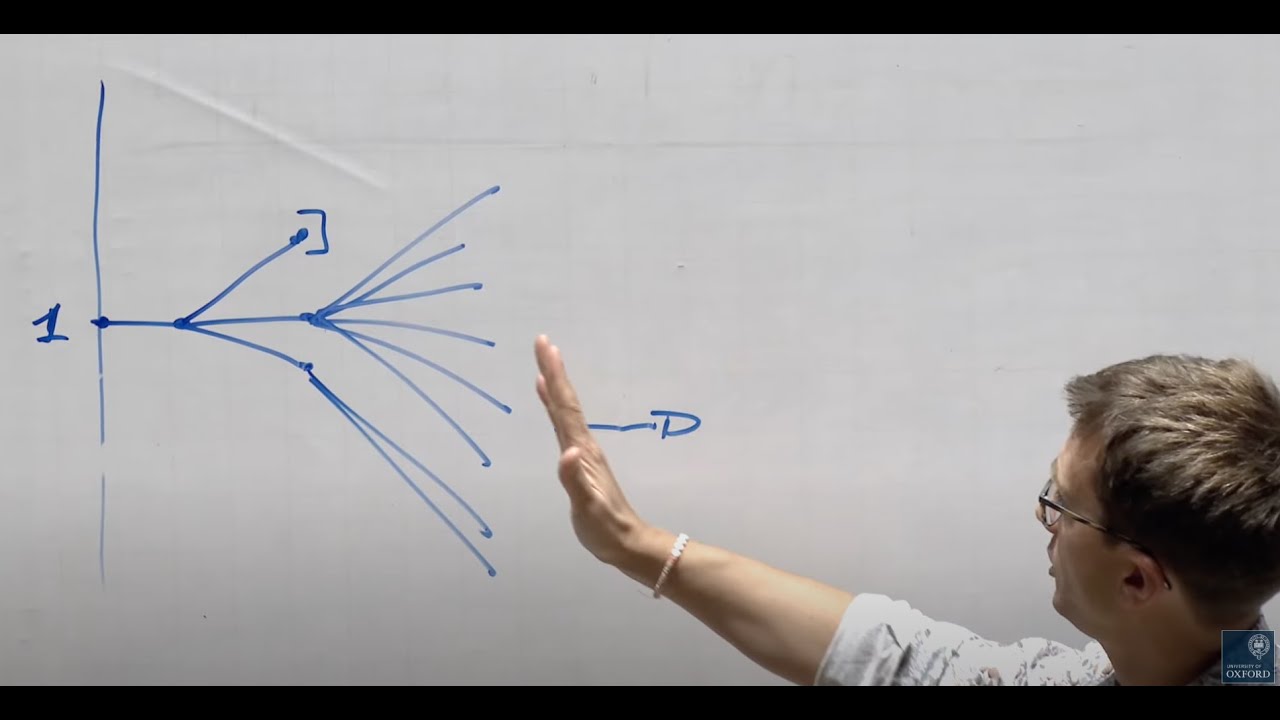
Co myslím větvícím procesem? Začínám s jedním jedincem a tento jedinec bude mít potomky. Takže možná měl jen jedno dítě. Pak ale tento jedinec také má potomky a možná měl tři děti. Toto dítě žádné potomky nemělo, zemřelo. Ale toto bylo velmi plodné a mělo spoustu dětí a toto možná mělo jen dvě. A tak dále.
Takže myšlenka je, že každý jedinec nebo bakterie, ať už je to cokoli, má určitý počet potomků. Všichni jsou na sobě nezávislí. Ale rozdělení počtu potomků je společné. A rádi bychom porozuměli, jak se tento proces chová v dlouhodobém horizontu, zda vymře nebo zda můžeme porozumět některým jemným vlastnostem tohoto Galtonova-Watsonova větvícího procesu.
Formální definice větvícího procesu
Definujme to správně matematicky. Moje definice byla, že Z₀ je 1. A co je Zₙ? Zₙ je počet jedinců v n-té generaci. A kolik jich je? Musím se podívat na předchozí generaci a pak umožnit každému z nich mít potomky. Takže potřebuji nějaké označení, a toto značení bude X. Co jsou X? Všechna X budou nezávislá stejně rozdělená. Mám tedy velké pole, XₙₖX. To jsou všechny nezávislé stejně rozdělené náhodné veličiny. Takže X₁₁ má rozdělení X. A toto je něco, co nabývá hodnot 0, 1, 2, atd. Pravděpodobnost, že X se rovná k, je rovna pₖ. Takže to je moje rozdělení.
Počet bakterií v n-té generaci - podívám se na všechny v n-1 generaci a umožním jim množit se. Takže toto je suma náhodných veličin. Ale počet náhodných veličin, které sčítám, je sám náhodný a je řízen počtem bakterií v předchozí generaci.
Generující funkce a pravděpodobnost vymření
Budu zkoumat tento proces pomocí generující funkce. Napíšu F nebo F_X(θ). Toto bude očekávání θ na X. Znáte tuto funkci. Studovali jsme tyto funkce. Toto je pravděpodobnostní funkce. Takže tím myslím sumu od k=0 do nekonečna, kde mám θᵏ·pₖ. Jaké jsou vlastnosti této funkce? F(1) je prostě očekávání 1 na X, takže to je 1. F(0) je podle konvence 0ˣ, což je buď 0, s výjimkou 0⁰, což bude 1. Takže to je p₀, pravděpodobnost, že nabývám hodnoty 0. A co F’(1)? Pokud to rozvinete, bude to rovno M, což je průměr X.
První tvrzení je, že pokud se podívám na funkci Fₙ(θ), která bude generující funkcí pravděpodobnosti Zₙ, tak tvrdím, že toto je n-tá iterace funkce F. Jak bychom to dokázali? F₁(θ) se rovná očekávání θᶻ¹. Toto je očekávání θˣ¹’¹. Moje Z₀ bylo 1. A tak se to rovná prostě F_X. A jsem hotov.
A co by bylo očekávání θᶻⁿ podmíněně na Zₙ₋₁ rovném k? Pokud vím, že jsem měl k jedinců v předchozí generaci, tento objekt, který byl sumou s náhodným počtem prvků, se nyní stává jen sumou k nezávislých stejně rozdělených náhodných veličin. Takže už nemám žádnou závislost na historii. Toto je rovno očekávání θˣⁿ¹ plus plus θˣⁿᵏ. A samozřejmě, nyní jsou všechny nezávislé. Takže to je jen očekávání θˣⁿ¹ krát… a všechny tyto jsou stejné. Toto není nic jiného než F(θ) na k-tou, protože každý z nich je F(θ).
Takže nyní mohu pozorovat, že mám toto k zde a měl jsem k tamhle. A co chci říct, je, že opravdu mohu považovat očekávání θᶻⁿ podmíněně na Zₙ₋₁. A to by mělo být samo o sobě náhodnou veličinou, která by měla být dána tímto vzorcem.
Pravděpodobnost vymření
Nechť Q je pravděpodobnost vymření. Nechť Q je pravděpodobnost, že Zₙ je rovno 0 pro nějaké n. Samozřejmě, pokud někdy vymřete, pak zůstanete vymřelí. V této hře není žádné vzkříšení. Takže to je totéž jako pravděpodobnost, že Zₙ je rovno 0 pro n dostatečně velké, kde dostatečně velké znamená od nějakého bodu dále.
Předpokládejme také, že p₁ je menší než 1. Pokud p₁ je rovno 1, znamená to, že vždy máte přesně jednoho potomka a populace je stále konstantní, vždy rovna jedné. To je velmi nudný případ.
Pokud toto platí, pak tvrdíme, že existují dvě možnosti. Pokud M je menší nebo rovno 1, pak Q je rovno 1. Takže populace vymře. A pokud M je větší než 1, pak Q je striktně menší než 1. Existuje pozitivní pravděpodobnost, že populace přežije navždy.
Co je důkaz? Důkaz je následující: Můžeme charakterizovat toto Q. Q je nejmenším kořenem rovnice F(Q) se rovná Q. Proč je to pravda? Pokud nechám Qₙ být pravděpodobností, že Zₙ je rovno 0, pak je to samozřejmě rostoucí funkce. To proto, že {Zₙ = 0} je menší množina než {Zₙ₊₁ = 0}. Jakmile jsem mrtvý, jsem mrtvý navždy, ale mohl bych být stále naživu a zemřít později. To znamená, že toto je rostoucí funkce.
Pravděpodobnost, že Z je rovno 0, není nic jiného než Fₙ(0), generující funkce pravděpodobnosti v 0. To je vlastnost, kterou jsme měli dříve. Takže toto je nyní totéž jako F(Fₙ₋₁(0)).
Martingaly a jejich aplikace v matematických financích
Nyní intuitivně, toto Q je rostoucí. Takže konverguje k něčemu. Je rostoucí a samozřejmě je menší nebo rovno jedné. Takže musí konvergovat k nějakému číslu. A nějak intuitivně by Qₙ mělo konvergovat k Q, pravděpodobnosti, že Zₙ je rovno 0 pro nějaké n, které bylo definováno dříve. Takže toto Qₙ se rovná F(Qₙ₋₁). Zatímco toto konverguje k Q, toto konverguje k F(Q). Takže to ukazuje, že Q musí řešit tuto rovnici.
Pokusme se vypočítat trochu více. Vypočítejme očekávání mé populace za předpokladu, že jsem měl k jedinců v předchozí generaci. To je snadné. To by bylo očekávání Xₙ₊₁,₁ + … + Xₙ₊₁,ₖ. A stejně jako dříve, tato znalost pro mě vlastně není důležitá, protože všechny tyto veličiny jsou nezávislé a stejně rozdělené, a díky linearitě očekávání bych doufal, že toto je stejné jako prosté očekávání. A pak by to mělo být jen k-krát očekávání X. Takže to je k-krát M.
Pokusme se udělat stejný trik jako předtím. Takže nyní napíšu očekávání Zₙ₊₁ za podmínky Zₙ = k. Takže to by mělo být M-krát Zₙ. A mohl bych v tom jaksi pokračovat. Mohl bych podmínit na Zₙ₋₁ atd. Zejména odtud vidím, že očekávání Zₙ₊₁ se rovná M-krát očekávání Zₙ, což se rovná M na druhou krát očekávání Zₙ₋₁ atd., což se rovná M na n+1.
Zkusme to normalizovat. Takže nechť Mₙ se rovná Zₙ děleno Mⁿ. Co se stane, když to udělám a vypočítám očekávání Mₙ za podmínky minulosti? Takže v minulosti to znamená, že znám všechny předchozí Mₙ, Mₖ, což je totéž jako znát předchozí Zₖ, protože toto je jen konstanta. Takže toto je očekávání Zₙ děleno Mⁿ za podmínky minulosti. Takže zejména znám předchozí hodnotu a to mi už říká, že to bude rovno M-krát Zₙ₋₁ děleno Mⁿ.
To se samozřejmě vykrátí a dostanu Mₙ₋₁. Takže to skutečně znamená, že jaksi moje nejlepší předpověď pro to, kde budu zítra, je dána vším, co se stalo dosud, což je to, kde jsem dnes.
Martingaly
Takový proces se bude nazývat martingal. Je to v názvu. Takže můžete hádat, že to bude pro nás důležité. Zejména budeme studovat konvergenci těchto procesů a uvidíme, že to musí konvergovat k M_∞, skoro jistě.
Nyní, pokud M je menší nebo rovno 1, pak vím, že Zₙ je rovno 0 pro n dostatečně velké. A samozřejmě, pokud Z je 0, pak M je také 0. Takže to znamená, že jediná limitní hodnota může být nula. A to je docela zajímavé, protože vidíte, že očekávání Mₙ se rovná 1, je nezávislé na n a jasně se nerovná očekávání limitu Mₙ, které bude v tomto případě rovno 0. To by vám mělo připomínat Fatouovo lemma v integraci.
Matematické finance
Pojďme si představit, že investujeme na akciovém trhu. Mám nějakou cenu akcie, Sₙ modeluje cenu akcie, a budu tyto akcie kupovat a prodávat. Co to znamená? Sedím zde v čase n a mám nějakou hotovost, možná moji hotovost nazývejme Vₙ. A pak mohu mít také nějaké akcie. Mohu se rozhodnout koupit akcie. Předpokládejme, že chci koupit Hₙ akcií.
Toto Hₙ by samozřejmě mohlo být funkcí minulosti, minulých cen. A pak čas pokračuje a dostanu se k n+1. Co se stane s hotovostí? Pokud jsem koupil tyto akcie, musel jsem si půjčit peníze, abych to udělal. To znamená, že jsem odečetl Hₙ krát Sₙ. To je kolik stálo Hₙ akcií v čase n. To by mohlo být kladné nebo záporné číslo. Takže buď dostávám úroky od banky, nebo platím úroky za půjčku. Ale předpokládejme, že existuje úroková sazba r. To znamená, že moje hotovost je nyní Vₙ minus Hₙ krát Sₙ krát (1+r). Buď můj dluh narostl, buď mi narostl úrok, nebo proti mně.
Co se stalo s mými akciemi? Nic se nestalo. Stále mám stejný počet akcií, ale nyní je mohu prodat. Takže pokud zkombiním tyto dvě pozice, znamená to, že moje nová hodnota, moje nová hotovost se bude rovnat tomuto. A pak +Hₙ krát Sₙ₊₁, protože prodávám za novou cenu.
Diskontované hodnoty a finanční oceňování
Přepišme to pomocí diskontovaných veličin. Nechť Ṽₙ je rovno (1+r)⁻ⁿ krát Vₙ. A podobně S̃ₙ bude (1+r)⁻ⁿ krát Sₙ. Toto (1+r)⁻ⁿ odpovídá hodnotě dnes jedné měnové jednotky za n časových období.
Typickou otázkou v matematických financích by bylo, jaká je spravedlivá cena dnes (n=0) za peněžní tok, nějakou platbu, řekněme F(S₀, S₁, …, Sₙ) v čase n. Kolik bych měl dnes zaplatit někomu, kdo je ochoten mi poskytnout nějakou náhodnou výplatu v budoucnosti?
Myšlenka od dob Blacka a Scholese by spočívala v tom, že se jedná o základní ekonomický zákon jedné ceny. Pokud máte dva způsoby, jak dosáhnout stejného peněžního toku, pak by měly mít stejnou cenu nebo stejnou hodnotu. Takže myšlenka je, že pokud existuje V₀ a H takové, že Vₙ se rovná F, což znamená, že mohu začít s nějakým kapitálem a pak použít obchodování s akciemi k replikaci tohoto budoucího peněžního toku, pak V₀ je spravedlivá cena. Pokud je někdo ochoten to prodat za méně, s radostí to koupím, vezmu si nějaké peníze, investuji do tohoto a replikuji. Takže ať už je to dražší nebo levnější, koupil bych nebo prodal. Ale mám jiný způsob, jak dosáhnout stejné výplaty za cenu V₀. A otázka je jak. Jak to vypočítat?
Ukazuje se, že pokud by S̃ byl martingal a já vzal očekávání a celá tato věc by zmizela a očekávání by bylo jen V₀, protože toto by opět bylo martingalem, stejně jako jsem to měl předtím.
Změna míry a replikační strategie
Předpokládejme, že existují dvě konstanty d≥0 takové, že 1-d < 1+r < 1+u a takové, že Sₙ je buď rovno (1-d) krát Sₙ₋₁ nebo (1+u) Sₙ₋₁. Co tady píšu? Jen píšu rekombinující strom. Začínám tady a jdu sem (1+u)S₀, (1-d)S₀, a pak jdu nahoru nebo dolů, dolů, nahoru atd. Tomu se říká binomický rekombinující strom. Pokaždé jdete stejným násobitelem dolů nebo nahoru.
Pak pro libovolné takové F existuje V₀ a H takové, že Vₙ je rovno F. A navíc existuje jedinečná míra pravděpodobnosti Q taková, že S̃ je Q-martingal a toto V₀ se rovná očekávání, nyní podle míry Q, (1+r)⁻ⁿF.
🔍 Kritické zhodnocení
Přednáška poskytuje komplexní úvod do pokročilého kurzu teorie pravděpodobnosti a představuje několik klíčových koncepcí, které budou v průběhu semestru rozvinuty. Přednášející efektivně propojuje elementární koncepty, které studenti již znají, s pokročilejšími myšlenkami, které teprve budou formálně definovány.
Silnou stránkou přednášky je její postupný přechod od jednoduché náhodné procházky přes různé úrovně sofistikovanosti při studiu konvergence (silný zákon velkých čísel, centrální limitní věta, zákon iterovaného logaritmu). Tento přístup poskytuje studentům jasnou představu o hierarchii výsledků v teorii pravděpodobnosti, což odpovídá modernímu chápání této disciplíny, jak je prezentováno například v učebnici “Probability: Theory and Examples” (Durrett, 2019).
Část o větvících procesech je obzvláště dobře strukturovaná a přednášející správně zdůrazňuje důležitost generujících funkcí při jejich studiu. Tato metodologie je standardní v literatuře, jak potvrzuje například Harris v “The Theory of Branching Processes” (2002) a novější přístupy v “Branching Processes: Variation, Growth, and Extinction of Populations” (Haccou, Jagers, Vatutin, 2005).
V části o martingalech a jejich aplikaci v matematickém financování přednášející představuje binomický model oceňování, který je základním stavebním kamenem pro složitější modely. Tento přístup je konzistentní s pedagogickou tradicí představenou Shreve v “Stochastic Calculus for Finance I: The Binomial Asset Pricing Model” (2004). Přednášející správně zdůrazňuje centrální roli martingalů a změny míry v teorii oceňování.
Co by mohlo být v přednášce rozvinuto více, je hlubší diskuse o podmíněném očekávání a jeho vlastnostech, které jsou klíčové pro pochopení martingalů. Williams v “Probability with Martingales” (1991) věnuje tomuto tématu značnou pozornost, protože je to základní koncept pro porozumění stochastickým procesům.
Zajímavé je, že přednášející zmiňuje historický vývoj silného zákona velkých čísel (od Bernoulliho po Kolmogorova), což poskytuje cenný kontext. Pro studenty, kteří mají zájem o historický vývoj pravděpodobnosti, by kniha “The Emergence of Probability” (Hacking, 2006) mohla poskytnout další vhled do tohoto historického vývoje.
Pro studenty, kteří chtějí lépe pochopit teorii míry jako základ pro pokročilou pravděpodobnost, kterou přednášející plánuje vybudovat v následujících přednáškách, by mohla být užitečná kniha “Measure Theory and Probability Theory” (Athreya, Lahiri, 2006), která se zaměřuje právě na budování teorie pravděpodobnosti na základech teorie míry.